Diện Tích Hình Vuông – Bí Quyết Tính Toán Chuẩn Xác

Diện tích hình vuông đóng vai trò là một trong những khái niệm hình học cốt lõi nhất mà bất kỳ ai cũng cần nắm vững để áp dụng vào thực tế cuộc sống. Việc hiểu thấu thấu đáo phương thức xác định không gian bên trong một hình tứ giác đều không chỉ giúp giải quyết các bài toán học đường mà còn hỗ trợ tối ưu trong việc phân chia mặt bằng. Để bắt đầu hành trình khám phá các thông số toán học thú vị này một cách chuyên sâu, hãy cùng đồng hành với thương hiệu Khí Phách.

Khái quát về diện tích hình vuông trong đời sống

Trong hệ thống hình học Euclid, khái niệm về vùng không gian nằm giới hạn bên trong bốn cạnh bằng nhau của một tứ giác đều luôn giữ một vị trí đặc biệt quan trọng. Khi chúng ta nhắc đến diện tích hình vuông, về bản chất, đó chính là kết quả của việc định lượng hóa toàn bộ bề mặt phẳng mà hình đó bao phủ trên một hệ tọa độ nhất định.

Việc xác định giá trị diện tích hình vuông không đơn thuần chỉ là một thao tác nhân số học giữa các đại lượng đo lường chiều dài đơn thuần. Trong các lĩnh vực kỹ thuật như kiến trúc hay lập trình đồ họa, chỉ số này còn đại diện cho mật độ phân bổ các đơn vị cơ bản, chẳng hạn như số lượng gạch lát trên một mặt sàn hoặc số điểm ảnh pixel hiển thị trên màn hình máy tính.

Dưới đây là bảng so sánh sự biến thiên của không gian bề mặt khi thay đổi kích thước cạnh mà bạn có thể tham khảo:

Độ dài cạnh đơn vị (m)	Diện tích hình vuông tương ứng (m2)	Tổng chiều dài đường biên (m)
5	25	20
12	144	48
20	400	80
35	1225	140

Phương pháp xác định diện tích hình vuông cơ bản

Phương pháp xác định diện tích hình vuông qua các thông số đại lượng

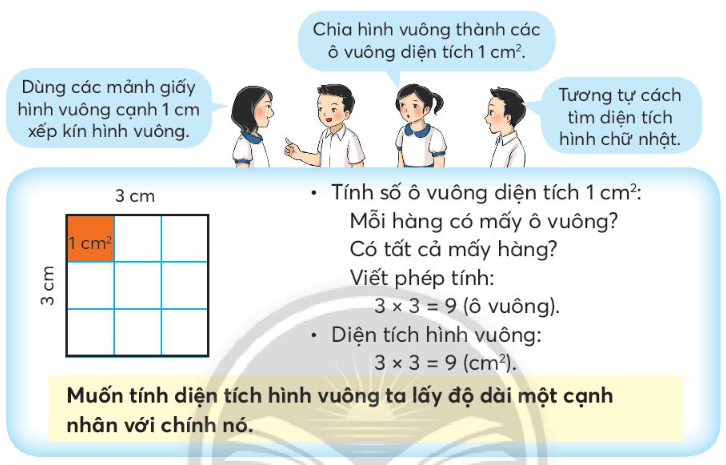
Sự linh hoạt trong toán học cho phép chúng ta tìm ra độ rộng bề mặt của một tứ giác đều thông qua nhiều dữ kiện đầu vào khác nhau thay vì chỉ phụ thuộc vào một yếu tố duy nhất. Khi bạn nắm bắt được mối quan hệ mật thiết giữa các bộ phận cấu thành hình học, việc tính toán diện tích hình vuông sẽ trở nên đơn giản hơn bao giờ hết dù dữ liệu đề bài cung cấp có phần hạn chế.

Dựa vào độ dài cạnh

Cách thức phổ biến và trực quan nhất chính là lấy trị số độ dài của một cạnh bất kỳ rồi thực hiện phép nâng lên lũy thừa bậc hai theo quy tắc nhân chính nó. Khi đó, kết quả thu được phản ánh chính xác vùng không gian phẳng bị chiếm chỗ bởi hình đó, đảm bảo sự thống nhất về đơn vị đo lường trong hệ thống tiêu chuẩn quốc tế hiện hành.

Tính qua đường chéo

Một phương án thay thế đầy hiệu quả khi không thể trực tiếp đo đạc các cạnh biên là tận dụng thông số đường nối giữa hai đỉnh đối diện của khối tứ giác. Biểu thức toán học cho phép chúng ta xác định diện tích hình vuông bằng cách bình phương độ dài đường chéo này, sau đó tiến hành phép chia cho hằng số hai để triệt tiêu phần dư thừa không thuộc phạm vi bề mặt.

Tính từ chu vi

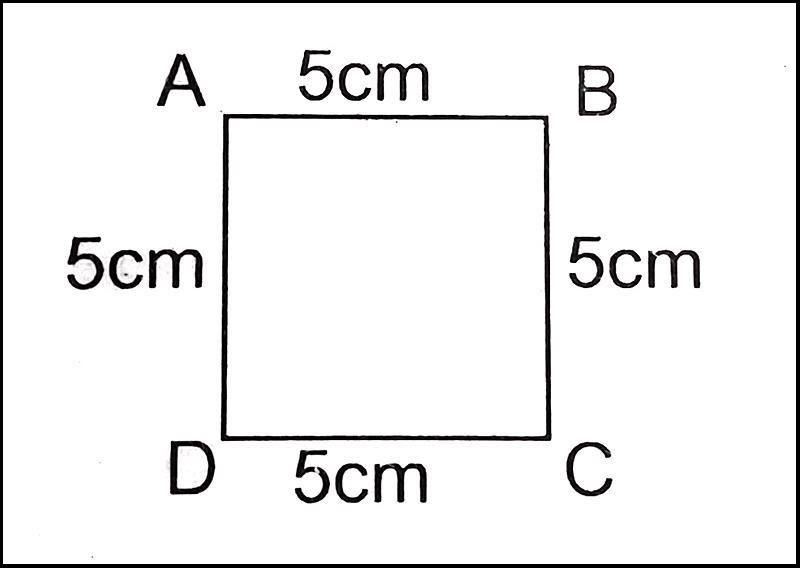
Nếu bạn chỉ sở hữu dữ liệu về tổng độ dài của bốn cạnh bao quanh, hãy thực hiện bước trung gian là chia con số đó cho bốn để tìm ra kích thước của một cạnh đơn lẻ. Ngay sau khi có được thông số cạnh, việc áp dụng phép nhân bình phương sẽ đưa ra đáp án cuối cùng về diện tích hình vuông mà bạn đang tìm kiếm một cách vô cùng chuẩn xác.

Dùng công thức lượng giác

Trong những trường hợp đặc biệt liên quan đến các góc xoay hoặc hệ tọa độ phức tạp, các nhà toán học còn có thể sử dụng hàm lượng giác để suy diễn không gian bề mặt. Tuy nhiên, cách tiếp cận này thường chỉ xuất hiện trong các giáo trình cao cấp hoặc lập trình mô phỏng không gian ba chiều phức tạp, nơi mà các đại lượng về cạnh không được biểu hiện trực tiếp.

Những ứng dụng thực tiễn của diện tích hình vuông trong đời sống

Trong thực tế, sự xuất hiện của các bề mặt tứ giác đều là vô cùng phổ biến, từ những vật dụng nhỏ bé hàng ngày cho đến các công trình kiến trúc đồ sộ mang tầm vóc quốc tế. Việc tính toán diện tích hình vuông mang lại những giá trị kinh tế trực tiếp, giúp tối ưu hóa nguồn lực và tránh lãng phí vật liệu trong các quy trình sản xuất công nghiệp hiện đại.

Dưới đây là những ví dụ điển hình về việc ứng dụng chỉ số không gian phẳng này vào các hoạt động thực tế:

• Quy hoạch mặt bằng xây dựng: Các kỹ sư thường chia nhỏ các khu đất thành những ô vuông chuẩn để dễ dàng quản lý mật độ xây dựng và phân bổ hạ tầng giao thông một cách khoa học nhất.
• Trang trí và thiết kế nội thất: Khi bạn cần tính số lượng gạch men để lát sàn, việc biết chính xác diện tích hình vuông của từng viên gạch sẽ giúp dự toán chi phí thu mua vật tư sát với thực tế.
• Công nghiệp dệt may: Trong quá trình cắt may các sản phẩm như khăn trải bàn hoặc thảm lót, các thợ may lành nghề luôn căn cứ vào số đo bề mặt để đảm bảo tính thẩm mỹ và tiết kiệm vải.
• Thiết kế linh kiện điện tử: Các con chip bán dẫn thường được bố trí trên các đế vuông, nơi mà việc tối ưu hóa không gian bề mặt giúp tăng cường khả năng xử lý dữ liệu và tản nhiệt hiệu quả hơn.
• Nông nghiệp công nghệ cao: Việc phân chia các luống cây theo ô vuông giúp nông dân dễ dàng tính toán lượng phân bón và nước tưới cần thiết cho từng đơn vị diện tích cụ thể.

Các lưu ý quan trọng để tính diện tích hình vuông chính xác

Dù công thức tính toán có vẻ đơn giản, nhưng trong quá trình thực hiện thực tế, rất nhiều người vẫn thường xuyên mắc phải những sai sót không đáng có dẫn đến kết quả sai lệch. Để đảm bảo giá trị diện tích hình vuông thu được có độ tin cậy cao, bạn cần phải đặc biệt chú trọng đến các yếu tố kỹ thuật và quy chuẩn về đơn vị đo lường trước khi đưa ra kết luận cuối cùng.

Thống nhất đơn vị đo

Một sai lầm kinh điển mà nhiều người gặp phải là thực hiện phép tính khi các cạnh đang ở những thang đo khác nhau, ví dụ như một cạnh tính bằng centimet và cạnh kia đo bằng mét. Trước khi bắt đầu xác định diện tích hình vuông, việc chuyển đổi tất cả các thông số về cùng một hệ quy chiếu là điều kiện tiên quyết để tránh những sai số khổng lồ có thể phá hỏng cả một dự án lớn.

Độ chính xác của dụng cụ

Trong các công trình yêu cầu sự tỉ mỉ, việc sử dụng các thiết bị đo laser hoặc thước dây chuyên dụng sẽ giúp hạn chế tối đa các sai số vật lý tác động lên kết quả. Bất kỳ một độ lệch nhỏ nào ở chiều dài cạnh cũng sẽ bị khuếch đại lên gấp nhiều lần khi chúng ta thực hiện phép tính bình phương để tìm ra diện tích hình vuông của đối tượng.

Phân biệt với các hình khác

Đôi khi một hình tứ giác nhìn bằng mắt thường có vẻ rất cân đối nhưng thực tế lại là hình thoi hoặc hình chữ nhật với độ lệch cạnh cực nhỏ. Bạn cần kiểm tra kỹ các góc vuông bằng ê-ke trước khi áp dụng công thức tính diện tích hình vuông, bởi nếu các góc không đạt 90 độ, mọi tính toán dựa trên quy tắc tứ giác đều sẽ trở nên vô nghĩa và không phản ánh đúng thực tế tại khí phách.

Kết luận

Diện tích hình vuông là một mấu chốt quan trọng giúp mở ra cánh cửa hiểu biết về thế giới hình học phẳng đầy thú vị và mang tính ứng dụng cao. Mong rằng những chia sẻ chi tiết phía trên đã giúp bạn tích lũy thêm những kiến thức bổ ích để áp dụng hiệu quả vào mọi khía cạnh của cuộc sống và công việc. Đừng quên tiếp tục theo dõi và ủng hộ những bài viết chuyên sâu khác từ cộng đồng kiến thức Khí Phách.