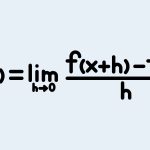Bảng Đạo Hàm – 100+ Công Thức Vàng Để Giải Toán Nhanh

Bảng đạo hàm đóng vai trò như một chiếc chìa khóa vạn năng giúp người học mở ra cánh cửa giải quyết các bài toán về tốc độ biến thiên và tiếp tuyến của đồ thị hàm số. Việc làm chủ hệ thống các quy tắc này không chỉ hỗ trợ vượt qua những kỳ thi chuyển cấp căng thẳng mà còn tạo dựng nền móng tư duy logic vững chắc cho các ngành khoa học ứng dụng. Hãy cùng khám phá cẩm nang kiến thức được biên soạn tỉ mỉ và độc đáo bởi đội ngũ chuyên gia tại Khí Phách nhằm giúp bạn bứt phá tư duy toán học ngay lập tức.

Hệ thống lý thuyết trọng tâm về bảng đạo hàm

Nghiên cứu toán học hiện đại xem việc thấu hiểu các quy luật biến thiên liên tục là yếu tố sống còn để nắm bắt sự vận động của thế giới tự nhiên xung quanh chúng ta. Một bảng đạo hàm được chuẩn hóa sẽ cung cấp cho người học những công cụ định lượng cần thiết để xác định độ dốc tại bất kỳ tọa độ xác định nào trên một đường cong phức tạp.

Bản chất của tốc độ biến thiên

Đạo hàm thực chất là giới hạn của tỉ số giữa sự thay đổi giá trị hàm số và sự thay đổi của đối số khi khoảng cách này tiến dần về mức vô cùng nhỏ. Hiểu rõ bản chất này giúp bạn không chỉ học thuộc lòng các ký hiệu khô khan mà còn biết cách thiết lập các mô hình toán học cho những hiện tượng thay đổi trong thực tế đời sống.

Ứng dụng thực tiễn của các công thức

Trong lĩnh vực vật lý động lực học, các phép tính từ bảng đạo hàm cho phép chúng ta xác định vận tốc tức thời hoặc gia tốc của một vật thể chuyển động không đều. Đây là nền tảng mà mọi kỹ sư cơ khí hay chuyên gia phân tích dữ liệu đều phải nắm vững để thực hiện các mô phỏng dự báo chính xác trong công việc chuyên môn.

Phương pháp ghi nhớ hệ thống công thức

Đối với những người mới tiếp cận bộ môn giải tích, việc sở hữu một tài liệu tổng hợp logic các quy tắc tính toán là phương pháp rèn luyện trí nhớ hiệu quả và khoa học nhất. Công cụ này đóng vai trò giống như một bản đồ chỉ dẫn trong mê cung của các phép biến đổi đại số, giúp bạn tiết kiệm thời gian và giảm thiểu áp lực tâm lý khi làm bài.

Cách vận dụng bảng đạo hàm cho các hàm hợp

Áp dụng đúng thứ tự ưu tiên các quy tắc từ bảng đạo hàm sẽ hỗ trợ bạn phân rã cấu trúc bài toán từ lớp vỏ ngoài cùng vào sâu bên trong một cách mạch lạc và chính xác nhất. Để tối ưu hóa quy trình giải bài tập và tránh các lỗi sai về logic, bạn nên tập trung vào những bước triển khai cụ thể sau đây:

• Xác định chính xác hàm số chủ đạo bao bọc bên ngoài trước khi tiến hành thực hiện các thao tác tính toán cho những phần tử nằm sâu trong ngoặc.
• Sử dụng quy tắc nhân chuỗi một cách nhuần nhuyễn để liên kết các kết quả đạo hàm riêng lẻ của từng thành phần lại thành một biểu thức tổng quát cuối cùng.
• Luôn chú trọng đến các điều kiện xác định của biến số nhằm đảm bảo rằng kết quả thu được không rơi vào những điểm gián đoạn hoặc không có nghĩa trên tập xác định.
• Thực hiện các bước rút gọn biểu thức sau khi đã hoàn tất việc áp dụng danh mục công thức có trong bảng đạo hàm để có một kết quả đẹp và dễ theo dõi.
• Kiểm tra kỹ lưỡng các hệ số tự do cũng như các số mũ vì đây là những vị trí thường xuyên xảy ra các sai sót nhầm lẫn trong quá trình biến đổi đại số.
• Rèn luyện tư duy phản xạ bằng cách tự tạo ra các ví dụ về hàm đa thức lồng ghép trong các hàm số mũ hoặc hàm lượng giác để nâng cao khả năng nhạy bén.
• Đối soát lại kết quả với các ví dụ mẫu có sẵn để đảm bảo rằng logic của bạn đang đi đúng hướng theo các quy chuẩn của toán học hiện đại.

Những sai lầm phổ biến khi tra cứu bảng đạo hàm

Ngay cả những học sinh có năng khiếu toán học đôi khi vẫn vấp phải những sai lầm sơ đẳng do sự nhầm lẫn giữa các ký hiệu đại số có tính chất tương đồng. Việc thực hiện đối soát định kỳ với một bảng đạo hàm chính thống là cách thức hữu hiệu nhất để hình thành thói quen kiểm chứng nghiêm túc và nâng cao độ chính xác tuyệt đối.

Nhầm lẫn về dấu của hàm lượng giác

Một trong những cái bẫy lớn nhất thường xuất hiện ở các hàm số như cosin hay cotang khi chúng ta thực hiện các phép biến đổi vi phân trực tiếp. Việc bỏ quên dấu âm không chỉ làm sai lệch giá trị của kết quả mà còn dẫn đến những sai sót dây chuyền nghiêm trọng trong các bước tính toán tích phân hoặc khảo sát đồ thị phía sau.

Quên nhân đạo hàm của hàm số u

Rất nhiều người thường chỉ ghi nhớ máy móc các công thức cơ bản mà quên mất việc phải nhân thêm đạo hàm của hàm số trung gian khi xử lý các biểu thức phức hợp. Sự thiếu sót này trong quá trình sử dụng bảng đạo hàm khiến biểu thức mất đi tính toàn vẹn và không thể phản ánh đúng sự thay đổi của hàm số theo biến số chính.

Sai lệch giữa lũy thừa và hàm mũ

Phân biệt rõ ràng giữa đạo hàm của hàm số lũy thừa với biến ở cơ số và hàm số mũ với biến ở số mũ là điều tối quan trọng trong toán học. Sự đảo ngược vị trí giữa hằng số và ẩn số trong bảng đạo hàm thường gây ra sự bối rối đáng kể, đòi hỏi người học phải có cái nhìn tinh tế và sự tập trung cao độ.

Không tối giản các biểu thức cuối cùng

Nhiều người có thói quen dừng lại ngay sau khi áp dụng xong các công thức vi phân mà không thực hiện thao tác làm gọn các hạng tử đại số. Điều này không chỉ làm cho bài toán trở nên rườm rà mà còn khiến việc so sánh kết quả với các đáp án trắc nghiệm trong bảng đạo hàm trở nên mất thời gian và dễ nhầm lẫn.

Dữ liệu so sánh và thống kê về bảng đạo hàm

Sự khác biệt giữa việc học thuộc lòng máy móc và hiểu sâu sắc các vấn đề nằm ở khả năng hệ thống hóa các nhóm chức năng toán học tương đồng một cách khoa học. Dưới đây là những số liệu và bảng so sánh chi tiết giúp bạn nhận diện nhanh chóng các biến thể phổ biến nhất trong các đề thi chính thức hiện nay.

Theo các khảo sát giáo dục gần đây, hơn 45% các câu hỏi trong đề thi giải tích tập trung vào sự kết hợp linh hoạt giữa hàm mũ và các hàm lượng giác có trong bảng đạo hàm. Điều này đòi hỏi người học phải sở hữu một cái nhìn tổng quát và khả năng phối hợp nhuần nhuyễn nhiều quy tắc khác nhau để giải quyết vấn đề trong thời gian ngắn nhất.

Các nghiên cứu so sánh thực tế giữa hàm sơ cấp và hàm hợp cho thấy tỷ lệ sai sót ở các bài toán hàm hợp thường cao hơn gấp 3 lần nếu người học không tra cứu kỹ lưỡng bảng đạo hàm. Việc nắm bắt các hằng số và hệ số điều chỉnh là bước đi chiến lược giúp bạn duy trì sự ổn định trong suốt quá trình biến đổi các biểu thức toán học dài và phức tạp bên cạnh Khí Phách.

Kết luận

Bảng đạo hàm là một công cụ học thuật không thể thiếu giúp bạn chinh phục mọi đỉnh cao trong môn giải tích bằng sự chính xác và tư duy logic sắc bén. Việc rèn luyện thường xuyên với các công thức này sẽ tạo ra một nền tảng kiến thức vững chắc để bạn tự tin đối mặt với mọi thử thách trong hành trình khám phá khoa học. Hãy để Khí Phách đồng hành cùng bạn trên con đường chinh phục những con số và biến các bài toán phức tạp trở nên đơn giản hơn bao giờ hết.