Công Thức Lượng Giác – Bí Quyết Giải Nhanh Toán 10 11 12

Công thức lượng giác vốn được xem là "xương sống" của môn Toán hình học và giải tích, đóng vai trò then chốt trong việc xử lý các phép biến đổi phức tạp. Việc nắm vững hệ thống dữ liệu này không chỉ hỗ trợ quá trình ôn thi chuyển cấp đạt kết quả cao mà còn xây dựng tư duy logic nhạy bén cho người học. Bạn hoàn toàn có thể chinh phục những bài tập hóc búa nhất nhờ vào lộ trình tổng hợp kiến thức từ chuyên trang Khí Phách.

Tổng quan về hệ thống công thức lượng giác cơ bản

Trong chương trình giáo dục phổ thông, việc tiếp cận với các khái niệm liên quan đến vòng tròn đơn vị và các giá trị sin, cos, tan, cot là bước đệm đầu tiên để hiểu về công thức lượng giác. Những định lý này không chỉ giới hạn trong sách vở mà còn là công cụ mô phỏng các hiện tượng tuần hoàn trong thiên nhiên, từ sóng âm cho đến sự vận động của các hành tinh.

Sự phân chia các nhóm công thức lượng giác giúp học sinh dễ dàng khu biệt được phương pháp giải toán theo từng dạng bài cụ thể. Thay vì cố gắng ghi nhớ một cách máy móc, việc hiểu rõ bản chất hình học của các tỉ số lượng giác sẽ tạo ra một nền tảng tư duy vững chắc, giúp bạn phản xạ nhanh chóng trước các đề thi có tính phân hóa cao.

Nhóm công thức lượng giác cộng và biến đổi nâng cao

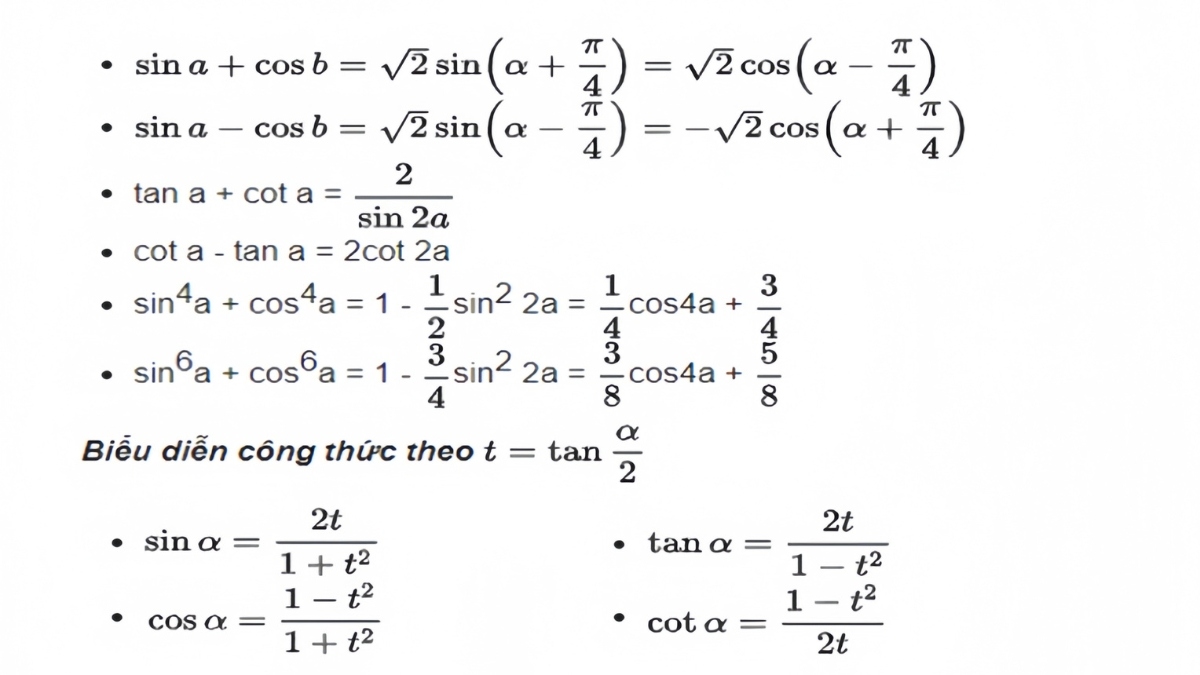
Việc vận dụng linh hoạt các biến thể của hàm số lượng giác đòi hỏi người học phải nắm chắc quy tắc chuyển đổi giữa các cung và góc đặc biệt. Khi thực hiện các phép tính tích phân hoặc đạo hàm phức tạp, nhóm công thức lượng giác này chính là "chìa khóa" vạn năng để tối giản biểu thức một cách nhanh nhất.

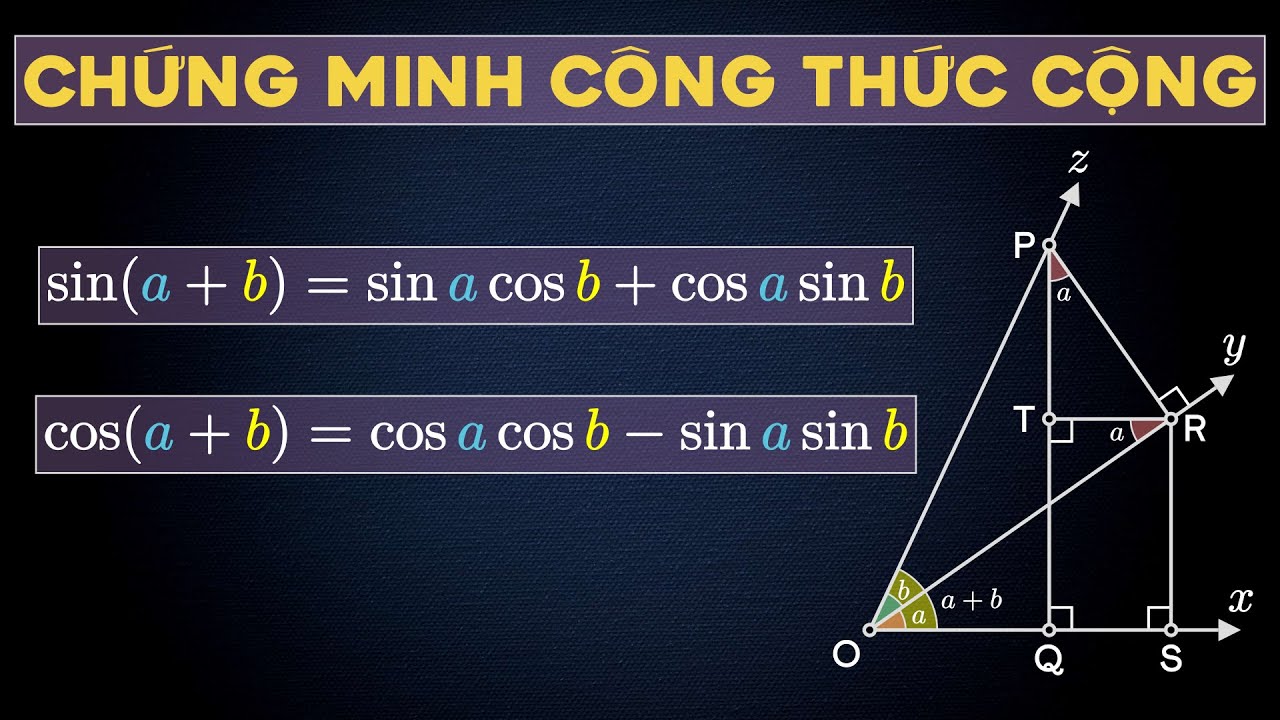
Hệ thức cộng cung

Đối với những góc không nằm trong bảng giá trị đặc biệt, chúng ta thường phân tách chúng thành tổng hoặc hiệu của hai góc quen thuộc để tính toán. Việc triển khai các hệ thức cộng giúp kết nối các giá trị hàm số của từng góc riêng lẻ vào một biểu thức thống nhất.

Phương pháp nhân đôi

Khi đối mặt với các góc có tỉ lệ gấp hai lần, kỹ thuật nhân đôi đóng vai trò quan trọng trong việc hạ bậc hoặc thu gọn các hàm số mũ cao. Đây là một trong những công thức lượng giác được sử dụng thường xuyên nhất trong các bài toán chứng minh đẳng thức.

Biến đổi tích thành tổng

Quá trình chuyển đổi từ tích của hai hàm số sang dạng tổng giúp đơn giản hóa các phép toán phân số và hỗ trợ tìm nguyên hàm hiệu quả hơn. Bạn cần lưu ý thứ tự của các hàm sin và cos để tránh nhầm lẫn về dấu trong quá trình thực hiện phép tính.

Công thức hạ bậc

Kỹ thuật hạ bậc thường được ứng dụng để đưa các biểu thức bậc cao về dạng bậc nhất, giúp việc giải phương trình lượng giác trở nên dễ dàng hơn. Nhóm công thức lượng giác này thường đi kèm với các bài toán yêu cầu tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số.

Góc (Radian)	Sin	Cos	Tan	Cot
0	0	1	0	Không xác định
π/6	1/2	√3/2	√3/3	√3
π/4	√2/2	√2/2	1	1
π/3	√3/2	1/2	√3	√3/3
π/2	1	0	Không xác định	0

Ứng dụng thực tế của các công thức lượng giác hiện nay

Kiến thức về toán học nói chung và công thức lượng giác nói riêng không chỉ tồn tại trên những trang giấy trắng mà còn hiện hữu trong mọi ngóc ngách của đời sống hiện đại. Dưới đây là một số ví dụ điển hình minh chứng cho sức mạnh của việc ứng dụng các lý thuyết toán học vào thực tế sản xuất và nghiên cứu:

• Xác định khoảng cách trong hàng hải và hàng không dựa trên tọa độ mặt cầu và các góc nghiêng.
• Thiết kế cấu trúc cầu đường, nhà cao tầng thông qua việc tính toán lực phân bổ và độ bền vật liệu bằng công thức lượng giác.
• Xử lý tín hiệu âm thanh và hình ảnh số trong công nghệ viễn thông bằng cách phân tích các sóng hình sin tuần hoàn.
• Ứng dụng trong y học để phân tích nhịp tim và các chỉ số sinh học thông qua đồ thị hàm số biến thiên.
• Phát triển các thuật toán trong trò chơi điện tử để mô phỏng chuyển động vật lý của nhân vật và môi trường xung quanh.
• Đo đạc diện tích địa hình và lập bản đồ địa lý dựa trên các tam giác lượng giác với độ chính xác cao.

Mẹo ghi nhớ công thức lượng giác nhanh và hiệu quả

Đối với nhiều người, việc học thuộc lòng hàng chục hệ thức khác nhau thường gây ra sự nhầm lẫn và nhanh quên sau một thời gian ngắn. Tuy nhiên, bằng cách áp dụng các mẹo ghi nhớ logic và sáng tạo, việc làm chủ các công thức lượng giác sẽ trở nên thú vị và nhẹ nhàng hơn rất nhiều.

Học qua thơ ca

Các thế hệ học sinh Việt Nam đã sáng tạo ra nhiều bài thơ lục bát hoặc những câu vè gieo vần để biến các ký hiệu khô khan thành lời ca dễ thuộc. Phương pháp này giúp não bộ ghi nhận thông tin một cách tự nhiên thông qua nhịp điệu thay vì cố gắng ép buộc ghi nhớ từng ký tự công thức lượng giác.

Dùng sơ đồ tư duy

Việc vẽ ra một bản đồ liên kết giữa các nhóm hệ thức sẽ giúp bạn có cái nhìn tổng quan về mối quan hệ giữa các hàm số. Khi nhìn vào sơ đồ, bạn sẽ thấy rõ sự chuyển hóa từ công thức lượng giác cơ bản sang các biến thể nâng cao, từ đó xây dựng được lộ trình giải toán logic.

Luyện tập thực tế

Không có phương pháp ghi nhớ nào hiệu quả bằng việc bắt tay vào giải các dạng bài tập đa dạng từ dễ đến khó một cách đều đặn. Thông qua quá trình va chạm với các tình huống giả định, bạn sẽ tự động khắc sâu các công thức lượng giác vào bộ nhớ dài hạn mà không cần tốn quá nhiều công sức khám phá thêm tại Khí Phách.

Kết luận

Công thức lượng giác không chỉ là những ký hiệu khô khan mà là công cụ vạn năng mở ra cánh cửa tri thức toán học rộng lớn cho nhân loại. Hy vọng bài viết này đã mang lại cái nhìn toàn diện và phương pháp học tập tối ưu để bạn tự tin vượt qua mọi kỳ thi sắp tới. Hãy tiếp tục trau dồi và cập nhật thêm nhiều kiến thức bổ ích khác tại chuyên trang giáo dục Khí Phách.