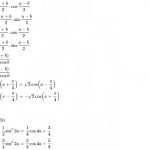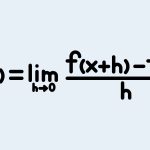Công Thức Nguyên Hàm – Chinh Phục Bài Toán Giải Tích

Công thức nguyên hàm chính là chìa khóa then chốt mở ra cánh cửa thấu hiểu các quy luật biến đổi phức tạp trong thế giới toán học hiện đại. Việc nắm vững các bảng tra cứu giá trị và phương pháp biến đổi không chỉ giúp tối ưu thời gian làm bài mà còn rèn luyện tư duy logic nhạy bén. Để hỗ trợ lộ trình ôn tập và nâng cao kiến thức cho người học, hệ thống thông tin của Khí Phách đã tổng hợp những nội dung cốt lõi và chuyên sâu nhất ngay dưới đây.

Khái niệm và giá trị của các công thức nguyên hàm

Trong chương trình toán học phổ thông và cao cấp, việc xác định một hàm số gốc từ đạo hàm của nó được coi là một hành trình đi ngược dòng thời gian của các con số. Bản chất của các công thức nguyên hàm không đơn thuần là sự ghi nhớ máy móc các ký hiệu mà là sự thấu hiểu về mối liên hệ mật thiết giữa sự thay đổi tức thời và giá trị tổng quát tích lũy.

Sự xuất hiện của hằng số C trong mọi kết quả tính toán không phải là một sự ngẫu nhiên mà nó đại diện cho một họ các đường cong song song trên mặt phẳng tọa độ. Mỗi giá trị C khác nhau sẽ tạo ra một thực thể riêng biệt nhưng đều có chung một đặc tính biến thiên tại mọi điểm xác định.

Các nhóm công thức nguyên hàm cơ bản thường gặp

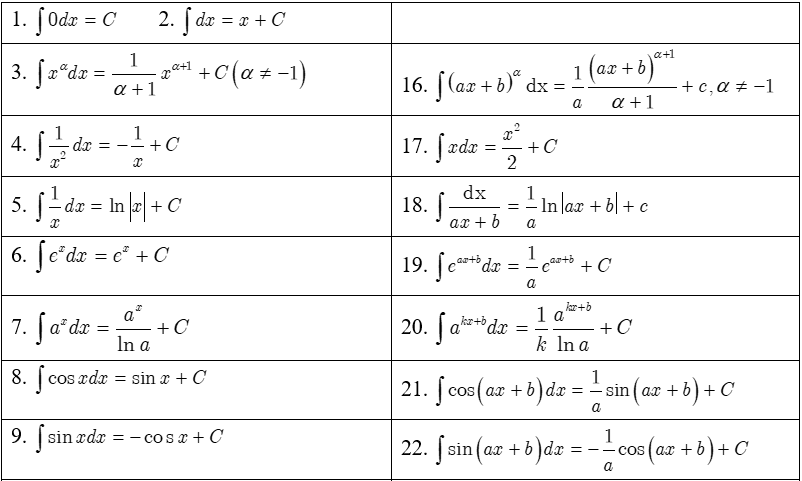
Việc phân loại các biểu thức toán học theo từng nhóm chức năng sẽ giúp quá trình truy xuất thông tin trong trí nhớ trở nên thuận tiện và chính xác hơn bao giờ hết. Thông thường, hệ thống các công thức nguyên hàm được chia thành các mảng riêng biệt như hàm đa thức, hàm lượng giác, hàm mũ và logarit để người học dễ dàng đối chiếu.

Hàm số đa thức

Các dạng lũy thừa của biến số luôn xuất hiện đầu tiên trong danh sách học tập vì tính trực quan và quy luật tăng bậc dễ hiểu. Khi áp dụng công thức nguyên hàm cho x mũ n, giá trị số mũ sẽ được nâng lên một đơn vị đồng thời chia cho chính chỉ số mới đó để đảm bảo tính cân bằng.

Hàm số lượng giác

Sự tuần hoàn của các hàm sin, cos hay tan tạo nên những biến đổi thú vị nhưng cũng dễ gây nhầm lẫn về dấu âm dương nếu không cẩn trọng. Việc thuộc lòng các công thức nguyên hàm lượng giác đòi hỏi bạn phải liên tưởng đến vòng tròn đơn vị và hướng di chuyển của các hàm số trong các cung phần tư khác nhau.

Hàm số mũ và logarit

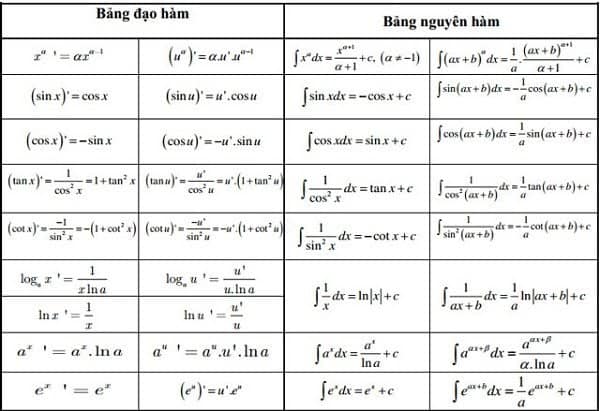
Sự tăng trưởng không ngừng của hàm e mũ x hay các hàm số mũ cơ số a thường là bài toán hóc búa trong các ứng dụng kinh tế và sinh học. Sử dụng chính xác công thức nguyên hàm cho nhóm này giúp xác định được tổng lượng tích lũy của một đại lượng sau một khoảng thời gian biến thiên liên tục.

Dưới đây là bảng tổng hợp các giá trị quan trọng giúp bạn tra cứu nhanh chóng trong quá trình thực hành bài tập:

Tên loại hàm số	Biểu thức đạo hàm f(x)	Kết quả nguyên hàm F(x) + C
Hàm số sơ cấp	0	C (Hằng số)
Hàm lũy thừa	x^n (n khác -1)	(x^(n+1)) / (n+1)
Hàm nghịch đảo	1/x	ln
Hàm lượng giác	sin(x)	-cos(x)
Hàm lượng giác	cos(x)	sin(x)
Hàm số mũ	e^x	e^x
Hàm mũ tổng quát	a^x	(a^x) / ln(a)

Kỹ thuật vận dụng công thức nguyên hàm nâng cao

Sau khi đã nắm vững các bảng giá trị cơ bản, việc bước vào những bài toán có cấu trúc phức tạp đòi hỏi các chiến thuật biến đổi linh hoạt và sắc sảo. Người học cần biết cách kết hợp nhiều bước trung gian để đưa một biểu thức lạ lẫm về dạng quen thuộc mà các công thức nguyên hàm tiêu chuẩn có thể giải quyết được.

• Phương pháp đổi biến số loại 1: Đặt một đại lượng phức tạp làm ẩn phụ u để đơn giản hóa biểu thức dưới dấu tích phân và áp dụng công thức nguyên hàm cơ bản.
• Kỹ thuật đổi biến số loại 2: Sử dụng các phép thế lượng giác hoặc hàm hyperbolic để xử lý các biểu thức chứa căn thức khó chịu một cách mượt mà.
• Nguyên hàm từng phần: Dựa trên quy tắc đạo hàm của một tích, phương pháp này cực kỳ hiệu quả khi đối mặt với sự kết hợp giữa hàm đa thức và hàm mũ hoặc lượng giác.
• Phân tích phân thức hữu tỷ: Chia tách các mẫu số phức tạp thành tổng của các phân số đơn giản giúp việc áp dụng công thức nguyên hàm logarit trở nên khả thi hơn.
• Sử dụng tính chất tuyến tính: Tách một biểu thức dài thành tổng các phần nhỏ để xử lý độc lập, giúp giảm bớt áp lực tính toán và tránh sai sót đáng tiếc.
• Nhận dạng vi phân: Quan sát nhanh mối liên hệ giữa các thành phần trong hàm số để đưa về dạng d(u), từ đó rút ngắn đáng kể các bước trình bày không cần thiết.

Những sai lầm cần tránh khi dùng công thức nguyên hàm

Trong quá trình giải toán, việc áp dụng máy móc các biểu thức mà không xem xét đến các điều kiện xác định thường dẫn đến những kết quả sai lệch hoàn toàn. Một trong những lỗi phổ biến nhất là bỏ quên hằng số C, điều này khiến câu trả lời chỉ là một trường hợp đơn lẻ thay vì là một họ nghiệm tổng quát theo đúng định nghĩa của công thức nguyên hàm.

Quên điều kiện của biến số

Mỗi công thức nguyên hàm đều có những khoảng xác định riêng biệt mà nếu vi phạm, biểu thức sẽ trở nên vô nghĩa trong tập số thực. Chẳng hạn, khi làm việc với hàm logarit tự nhiên, việc đảm bảo biểu thức bên trong dấu trị tuyệt đối luôn dương là một yêu cầu bắt buộc không thể bỏ qua.

Nhầm lẫn giữa đạo hàm và nguyên hàm

Nhiều người thường bị rối loạn trong việc đảo ngược các quy tắc tính toán, đặc biệt là với các hàm số lượng giác cơ bản. Việc nhầm lẫn giữa việc thêm dấu trừ cho sin hay cos khi áp dụng công thức nguyên hàm có thể phá hỏng toàn bộ logic của một bài toán dài.

Bỏ sót các hệ số của hàm hợp

Khi đối mặt với hàm số có dạng f(ax+b), việc quên chia cho hệ số a là lỗi sai kinh điển khiến kết quả bị sai lệch theo cấp số nhân. Luôn ghi nhớ quy tắc đưa hệ số ra ngoài khi sử dụng các biến thể của công thức nguyên hàm mở rộng để đảm bảo tính đúng đắn cho bài giải.

Kết quả của việc vận dụng đúng công thức nguyên hàm sẽ mang lại sự nhất quán trong các bước suy luận và giúp bạn tiếp cận các kiến thức về tích phân xác định một cách dễ dàng hơn. Sự tỉ mỉ trong từng chi tiết nhỏ chính là yếu tố phân loại trình độ của người học trong các kỳ thi cạnh tranh khốc liệt tại khí phách.

Kết luận

Công thức nguyên hàm là một phần không thể tách rời của toán học ứng dụng, giúp chúng ta giải mã các vấn đề từ vật lý lý thuyết đến tài chính thực nghiệm. Việc kiên trì rèn luyện và áp dụng các bảng tính này vào thực tế sẽ giúp bạn xây dựng một nền tảng tư duy vững chắc và tự tin. Hãy tiếp tục theo dõi các bài viết chuyên sâu trên Khí Phách để trang bị cho mình những kỹ năng giải toán ưu việt và hiệu quả nhất.