Hình Bình Hành – Tổng Hợp 8 Kiến Thức Quan Trọng Nhất

Hình bình hành là một dạng tứ giác đặc biệt trong không gian hai chiều mang những đặc tính đối xứng và song song vô cùng thú vị. Việc thấu hiểu bản chất của cấu trúc này không chỉ hỗ trợ quá trình học tập mà còn mở ra những tư duy logic trong thiết kế kỹ thuật. Những thông tin chuyên sâu dưới đây được tổng hợp và biên soạn bởi đội ngũ am hiểu tại Khí Phách.

Tìm hiểu về khái niệm hình bình hành cơ bản

Trong thế giới của các đa giác, một tứ giác được định danh là hình bình hành khi và chỉ khi nó sở hữu hai cặp cạnh đối diện nằm trên các đường thẳng song song tuyệt đối. Điều này có nghĩa là các đoạn thẳng đối diện sẽ duy trì một khoảng cách cố định và không bao giờ giao cắt nhau dù có kéo dài vô tận về hai phía.

Xét về mặt lịch sử toán học, khái niệm về hình bình hành đã xuất hiện từ rất sớm trong các công trình của Euclid, nơi ông mô tả về sự tương quan giữa các đường thẳng không gặp nhau. Đặc trưng lớn nhất của loại hình này chính là sự bình đẳng về độ dài giữa các cặp cạnh đối diện, tạo ra một sự hài hòa về mặt diện tích và chu vi.

Khái niệm và định nghĩa về đa giác hình bình hành

Dấu hiệu nhận biết hình bình hành chính xác nhất

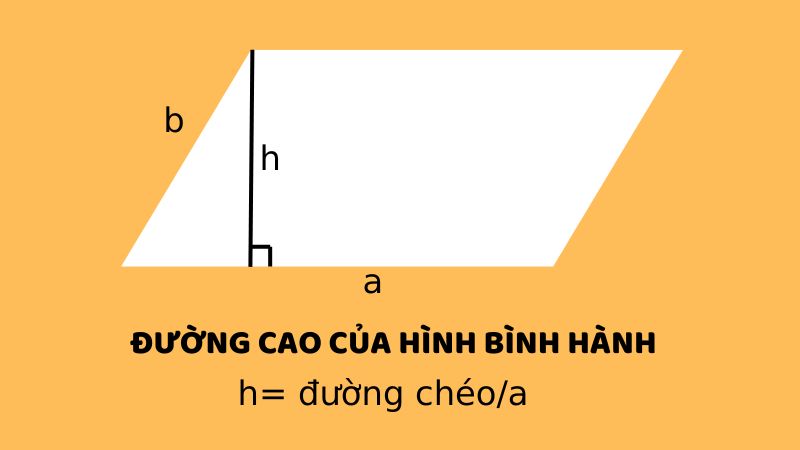
Để xác định một tứ giác bất kỳ có thuộc nhóm này hay không, bạn cần dựa vào một loạt các tiêu chuẩn hình học khắt khe. Những quy tắc này đảm bảo rằng mọi thuộc tính nội tại của đối tượng đều thỏa mãn điều kiện song song và bằng nhau.

Các cặp cạnh đối song song

Khi bạn quan sát thấy một tứ giác có hai cặp cạnh đối diện cùng song song với nhau, đó chắc chắn là một hình bình hành. Sự song song này thường được chứng minh thông qua các cặp góc so le trong hoặc góc đồng vị bằng nhau khi có một đường thẳng thứ ba cắt qua.

Các cặp cạnh đối bằng nhau

Một tiêu chí quan trọng khác chính là độ dài của các đoạn thẳng đối diện phải hoàn toàn tương đồng về giá trị đại số. Nếu một tứ giác thỏa mãn việc các cạnh đối diện có chiều dài bằng nhau từng đôi một, nó sẽ tự động hình thành nên cấu trúc của một hình bình hành.

Các cặp góc đối bằng nhau

Về phương diện góc độ, tổng các góc trong của loại hình này luôn bằng 360 độ, nhưng đặc biệt hơn là các góc nằm đối diện nhau phải có số đo giống hệt nhau. Sự phân bổ góc này tạo nên tính đối xứng tâm, một đặc trưng không thể thiếu khi nghiên cứu về hình bình hành trong toán học cao cấp.

Công thức tính toán trong hình bình hành chi tiết

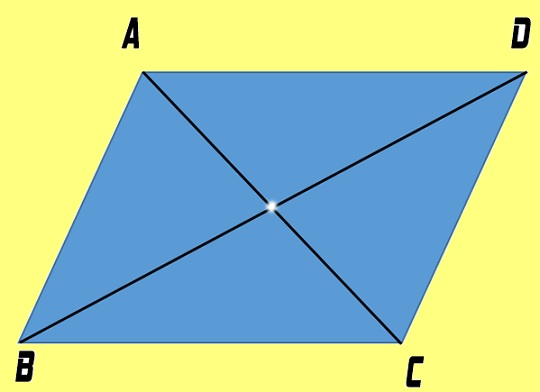
Việc tính toán các thông số định lượng đòi hỏi sự chính xác tuyệt đối trong việc áp dụng các biểu thức toán học đã được chứng minh. Dưới đây là những quy tắc cốt lõi giúp bạn xác định kích thước của đối tượng này một cách nhanh chóng.

• Để tìm chu vi, chúng ta tiến hành lấy tổng độ dài của hai cạnh kề nhau rồi nhân đôi kết quả thu được.
• Diện tích của hình bình hành được xác định bằng tích của một cạnh đáy với chiều cao vuông góc hạ xuống cạnh đó.
• Trong trường hợp biết độ dài hai cạnh và góc xen giữa, diện tích còn có thể tính bằng tích hai cạnh nhân với sin của góc đó.
• Độ dài đường chéo có mối liên hệ mật thiết với các cạnh thông qua định lý hàm số cos trong tam giác cấu thành.
• Tổng bình phương độ dài hai đường chéo luôn bằng tổng bình phương độ dài bốn cạnh của hình bình hành đó.
• Khi thực hiện tính toán, hãy đảm bảo tất cả các đơn vị đo lường đã được quy đổi về cùng một hệ tiêu chuẩn duy nhất.

Ứng dụng thực tiễn của hình bình hành đời sống

Không chỉ dừng lại ở những trang sách, cấu trúc này hiện diện mạnh mẽ trong mọi ngóc ngách của cuộc sống từ công nghiệp đến nghệ thuật. Sự linh hoạt trong việc thay đổi góc độ mà vẫn giữ nguyên độ dài cạnh khiến hình bình hành trở thành lựa chọn tối ưu cho nhiều thiết kế cơ khí.

Để hiểu rõ hơn về sự khác biệt giữa các loại hình, hãy cùng theo dõi bảng so sánh các thông số đặc trưng ngay dưới đây:

Đặc điểm so sánh	Hình bình hành thông thường	Hình chữ nhật	Hình thoi
Các cạnh đối song song	Luôn luôn có	Có	Có
Bốn cạnh bằng nhau	Không bắt buộc	Không bắt buộc	Luôn luôn có
Các góc vuông	Không có	Có 4 góc vuông	Không bắt buộc
Hai đường chéo vuông góc	Không	Không	Có
Tính chất hình bình hành	Là tính chất gốc	Có đầy đủ	Có đầy đủ

Trong thiết kế kiến trúc

Các kiến trúc sư thường xuyên sử dụng cấu trúc này để tạo ra các hiệu ứng thị giác độc đáo trên bề mặt tòa nhà hoặc các hệ thống mái che di động. Khả năng biến dạng linh hoạt giúp cấu trúc hình bình hành chịu được các lực tác động từ gió và áp lực môi trường tốt hơn so với các hình khối cứng nhắc.

Trong kỹ thuật cơ khí

Bạn sẽ dễ dàng tìm thấy mô hình này trong các cơ cấu nâng hạ như kích xe ô tô hay các cánh tay robot công nghiệp. Nhờ tính chất các cạnh đối luôn song song, cơ cấu hình bình hành cho phép nâng vật nặng lên cao theo phương thẳng đứng mà không làm thay đổi hướng của vật thể.

Trong mỹ thuật đồ họa

Các nhà thiết kế thường tận dụng hình khối này để tạo ra chiều sâu không gian và phối cảnh trong các tác phẩm 2D và 3D. Việc xoay chuyển các trục của hình bình hành giúp tạo ra cảm giác về sự chuyển động và tốc độ, làm cho hình ảnh trở nên sống động và bắt mắt hơn đối với người xem bên cạnh khí phách vn.

Kết luận

Hình bình hành không chỉ đơn thuần là một chủ đề toán học mà còn là một công cụ tư duy sắc bén trong nhiều lĩnh vực quan trọng của xã hội. Hy vọng rằng những phân tích chuyên sâu phía trên đã cung cấp cho bạn cái nhìn thấu đáo và toàn diện về loại tứ giác đặc biệt này. Hãy tiếp tục khám phá thêm nhiều kiến thức bổ ích khác cùng với Khí Phách trong những bài viết sắp tới.