Thể tích hình hộp chữ nhật: công thức dễ nhớ, ví dụ

Thể tích hình hộp chữ nhật tưởng như chỉ là một phép nhân, nhưng thực ra nó giúp bạn “đo sức chứa” của những thứ rất quen như thùng carton, bể nước, ngăn tủ hay cả một căn phòng. Khi nhìn thể tích như lượng không gian mà vật thể chiếm trong ba chiều, bạn sẽ thấy công thức gắn với việc xếp đầy các khối lập phương đơn vị, nên nhớ theo kiểu hiểu chứ không phải thuộc.

Nếu bạn hay nhầm giữa diện tích và thể tích, hoặc cứ gặp đổi đơn vị là loay hoay, hãy học Thể tích hình hộp chữ nhật theo một đường thẳng: hiểu khái niệm, dùng công thức, rồi tự kiểm tra lại kết quả bằng vài mẹo nhỏ. Mình sẽ ưu tiên câu mạch lạc và có hình dung, để bạn đọc xong có thể áp dụng ngay mà không phải “học lại từ đầu”. Quan trọng là bạn kiểm soát được từng bước, thay vì làm theo quán tính rồi hy vọng ra đáp án đúng.

Thể tích hình hộp chữ nhật là gì và dùng khi nào

Trong hình học không gian, Thể tích hình hộp chữ nhật là số khối lập phương đơn vị có thể xếp kín bên trong khối hộp, nên nó phản ánh mức độ “chiếm chỗ” của vật thể theo ba chiều. Nếu tăng mỗi kích thước lên một chút thì sức chứa tăng rất nhanh, vì kết quả chịu tác động đồng thời của dài, rộng và cao. Chính vì tính “nhạy” này, thể tích thường được dùng để so sánh sức chứa một cách công bằng.

Bạn gặp dạng bài này vì khối hộp chữ nhật là mô hình của nhiều đồ vật thật, và chỉ cần tính đúng là có thể ước lượng dung tích hay lượng vật liệu cần dùng. Tuy nhiên, khi làm Thể tích hình hộp chữ nhật trong đề kiểm tra, người học hay sai vì đọc thiếu dữ kiện, chọn nhầm kích thước hoặc quên đổi đơn vị, rồi đến dòng cuối mới “giật mình”. Trước khi tính, hãy thử nói thành lời: “mình đang cần dài–rộng–cao của khối này”, nghe đơn giản nhưng cực hiệu quả.

Nhận diện kích thước và đơn vị trước khi tính

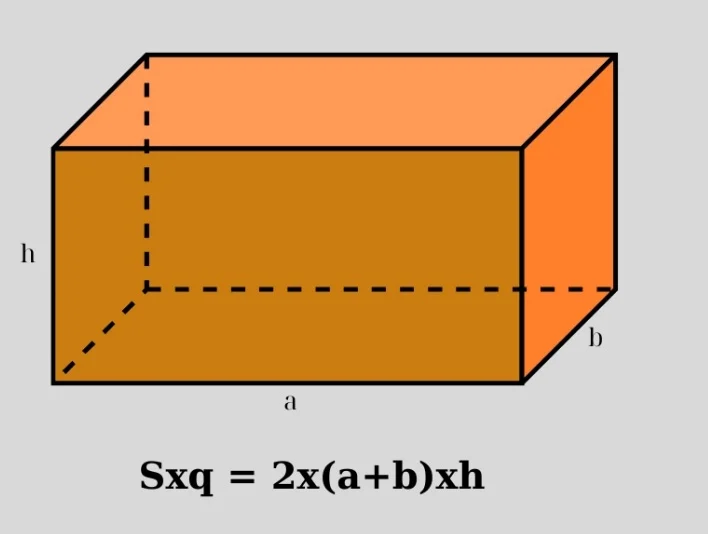
Khi làm Thể tích hình hộp chữ nhật, bạn cần ba kích thước khác phương: dài, rộng, cao, và chúng phải vuông góc với nhau, nên hãy tránh lấy nhầm hai cạnh nằm cùng hướng trên một mặt. Một cách kiểm nhanh là nhìn xem “chiều cao” có vuông góc với mặt đáy bạn chọn hay không, vì hình vẽ phối cảnh dễ khiến bạn tưởng nhầm cạnh nghiêng là chiều cao. Nếu đề có hình, bạn có thể ký hiệu a, b ở đáy và h theo phương thẳng đứng để giữ nhịp suy nghĩ.

Về đơn vị, thể tích dùng cm³, dm³, m³… và bạn chỉ thật sự an toàn khi mọi kích thước đã cùng một hệ, như cùng cm hoặc cùng m, rồi mới thay vào công thức. Hãy nhớ rằng đổi một bậc đơn vị thể tích tương ứng nhân hoặc chia 1000, vì có ba chiều, nên đừng đổi xong một cạnh rồi vội nhân ngay. Ví dụ, 0,5 m³ = 500 dm³, thường dễ hình dung hơn khi quy về dung tích.

Thể tích hình hộp chữ nhật: công thức và cách suy luận

Công thức của Thể tích hình hộp chữ nhật là V = dài × rộng × cao, và lý do nằm ở cách “đếm theo lớp”: mặt đáy tạo ra một lưới gồm dài × rộng ô vuông đơn vị, mỗi ô ứng với một cột khối lập phương. Khi bạn xếp các cột đó lên đến chiều cao cần thiết, tổng số khối lập phương đơn vị chính là tích của ba kích thước. Từ đây, bạn cũng thấy ngay mối liên hệ quen thuộc: “diện tích đáy” nhân “chiều cao”.

Với Thể tích hình hộp chữ nhật, khi đã hiểu gốc, bạn sẽ linh hoạt với đề bài cho dữ kiện gián tiếp, vì bạn biết mình đang tìm “một lớp” rồi nhân số lớp, nên chỉ cần đổi cách biểu diễn chứ không đổi bản chất. Đồng thời, hãy cảnh giác với đường chéo mặt hoặc đường chéo không gian, bởi chúng không thể thay trực tiếp cho một cạnh nếu chưa biến đổi. Gặp từ “đường chéo”, hãy nghĩ tới Pythagore như một chiếc phanh an toàn để xác định lại cạnh thật.

V=a×b×h và biến thể S×h trong bài thực tế

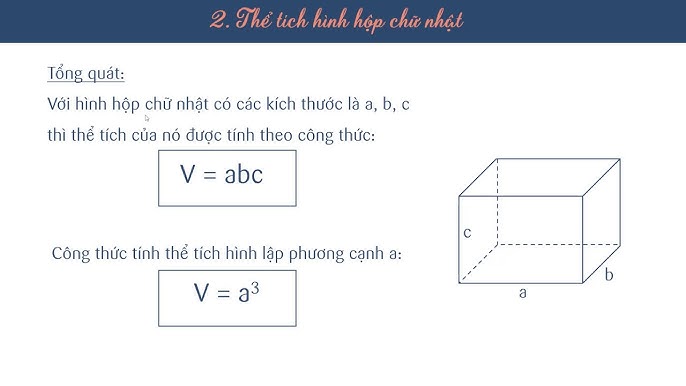
Trong bài tập, Thể tích hình hộp chữ nhật thường viết gọn V = a × b × h, với a và b là hai cạnh đáy, còn h là chiều cao, và cách viết này giúp bạn nhìn rõ cấu trúc: a × b là diện tích một lớp đáy, nhân thêm h là xếp chồng lớp đó lên h lần. Nếu đề cho diện tích đáy S sẵn, bạn dùng V = S × h để khỏi vòng qua nhiều bước, miễn là xác định đúng mặt đáy và đúng chiều cao vuông góc. Thói quen ghi “đáy là mặt nào” làm lời giải sáng sủa và hạn chế nhầm lẫn.

Khi áp dụng vào đời sống, bạn có thể đổi kết quả sang đơn vị quen hơn, chẳng hạn 1 dm³ tương đương 1 lít, nên con số “khối” trở thành dung tích dễ hình dung. Nếu kết quả nghe quá vô lý, hãy quay lại kiểm tra đơn vị và xem mình có lỡ dùng nhầm đường chéo hay không, vì sai kiểu này thường tạo ra con số “lạc quẻ” ngay từ đầu. Bạn cũng có thể ước lượng bằng cách làm tròn kích thước, để đoán khoảng giá trị trước khi tính chính xác.

Thể tích hình hộp chữ nhật trong bài tập: quy trình và mẹo

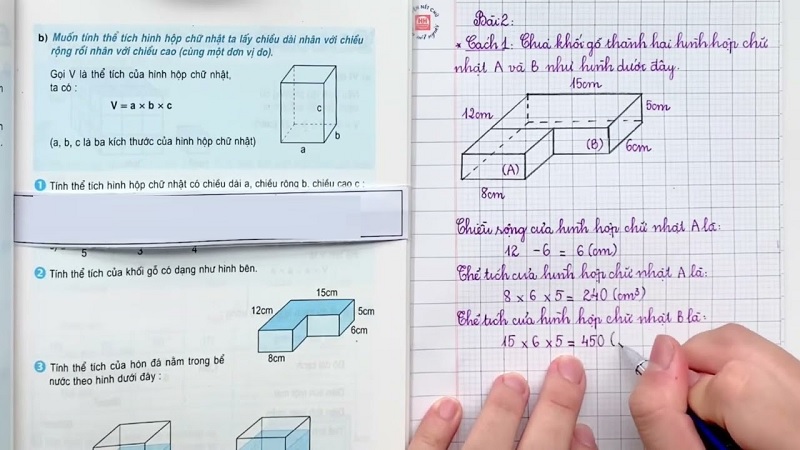
Để giải bài về Thể tích hình hộp chữ nhật ổn định, bạn có thể theo ba bước: xác định đúng ba kích thước vuông góc, thống nhất đơn vị, rồi mới thay vào công thức và tính. Bước đầu là nơi dễ trượt nhất khi đề đưa thêm đoạn thẳng phụ, nên đừng ngại viết a, b, h ra giấy như một “checklist” nhỏ để giữ nhịp. Chậm một chút ở phần đọc đề sẽ giúp bạn nhanh hơn ở phần tính toán.

Sau khi tính xong, hãy kiểm tra Thể tích hình hộp chữ nhật bằng so sánh nhanh: giữ đáy mà tăng chiều cao thì thể tích phải tăng, còn nếu một kích thước rất nhỏ thì kết quả khó mà lớn bất thường. Cuối cùng, nhìn lại đơn vị ở dòng kết luận, vì chỉ cần thấy m² hay cm² xuất hiện là biết bạn đang lẫn sang diện tích, và đây là lỗi phổ biến nhất khi làm bài gấp.

Tránh lỗi đổi đơn vị và kiểm tra đáp án nhanh

Lỗi đổi đơn vị hay gặp là bạn đổi 0,2 m thành 20 cm đúng, nhưng lại quên đổi các kích thước còn lại cho đồng bộ, hoặc quên rằng thể tích là đơn vị khối nên không thể “đổi một chiều rồi thôi”. Một mẹo là luôn viết đơn vị cạnh mỗi số và chỉ cho phép mình thay số vào công thức khi ba kích thước đã cùng một hệ, như cùng cm hoặc cùng m. Khi đề cho số thập phân, bạn có thể chọn hệ đơn vị khiến phép nhân gọn hơn, miễn là bạn nhất quán bên cạnh Khí Phách.

Khi đã có đáp án, hãy thử thế ngược lại để kiểm: nếu đang tìm một cạnh, lấy thể tích chia cho tích hai cạnh còn lại xem có ra đúng số đã suy ra không, và nếu đề so sánh hai khối hộp, kiểm xem khối nào có đáy lớn hoặc cao hơn thì kết quả có phản ánh đúng xu hướng không. Nếu mọi thứ “khớp” cả về phép tính lẫn trực giác, bạn có thể chốt Thể tích hình hộp chữ nhật mà không phải lăn tăn. Luyện thêm vài bài tự đặt số liệu, ví dụ thay đổi một kích thước rồi quan sát thể tích đổi ra sao, sẽ giúp phản xạ của bạn nhanh lên rõ rệt.