Thể Tích Khối Trụ – Công Thức Và Cách Tính Chính Xác

Thể tích khối trụ đóng vai trò như một thước đo định lượng không gian mà một vật thể có dạng hình trụ chiếm giữ trong môi trường ba chiều. Việc am hiểu các phương thức đo đạc này giúp chúng ta dễ dàng thiết kế các bể chứa hoặc tính toán nguyên vật liệu trong xây dựng một cách tối ưu. Mời bạn cùng tìm hiểu những thông tin chuyên sâu về chủ đề toán học ứng dụng đầy thú vị này tại hệ thống Khí Phách.

Tìm hiểu tổng quan về thể tích khối trụ trong đời sống

Khái niệm về không gian bên trong của một hình trụ tròn xoay xuất phát từ việc xác định diện tích mặt đáy kết hợp với chiều dài trục đứng. Trong môi trường thực tế, chúng ta thường xuyên bắt gặp các vật dụng có cấu trúc này như đường ống dẫn nước, lon nước giải khát hay các cột trụ bê tông cốt thép vững chãi.

Việc xác định thể tích khối trụ không chỉ dừng lại ở các bài toán trên trang giấy mà còn mở rộng ra quy trình quản lý chất lỏng trong công nghiệp hóa chất. Khi hiểu rõ cấu trúc của một khối tròn dài, bạn sẽ nắm bắt được cách thức chuyển đổi giữa các đơn vị đo lường khác nhau từ mét khối sang lít hoặc mililit.

Công thức chuẩn xác nhất để tính thể tích khối trụ

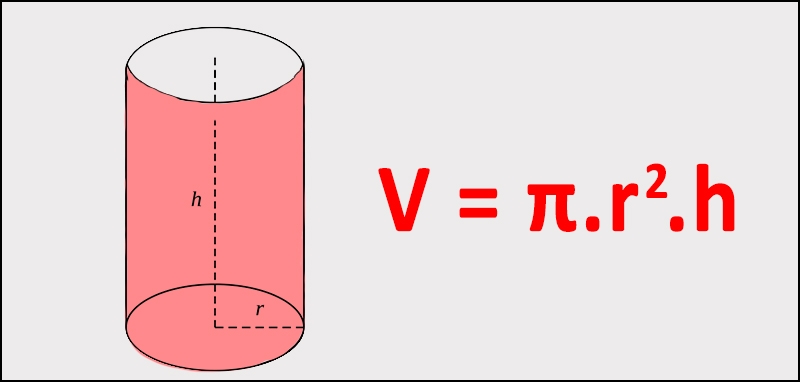
Để xác định chính xác dung tích của một vật thể hình trụ, chúng ta dựa trên mối liên hệ giữa bán kính mặt tròn và chiều cao nối hai đáy. Biểu thức toán học này được xây dựng trên nguyên lý xếp chồng vô số các mặt tròn đồng nhất lên nhau theo một đường thẳng đứng cố định.

Hằng số pi quan trọng

Giá trị số pi đóng vai trò then chốt trong việc giải mã các phép tính liên quan đến đường tròn và mặt phẳng cong. Thông thường, số 3,14 được ưu tiên sử dụng để đơn giản hóa các bước làm bài nhưng vẫn đảm bảo độ tin cậy.

Bán kính đáy hình trụ

Khoảng cách từ tâm điểm đến đường biên của mặt tròn đáy được ký hiệu là r và là thành phần không thể thiếu. Khi bạn nâng bậc hai giá trị này, chúng ta sẽ có được diện tích bề mặt tiếp xúc của khối vật thể với mặt phẳng ngang. Lưu ý rằng đường kính phải được chia đôi trước khi đưa vào công thức thể tích khối trụ để tránh những nhầm lẫn đáng tiếc.

Chiều cao của khối

Đoạn thẳng vuông góc nối liền tâm của hai mặt đáy chính là chiều cao h của hình trụ mà chúng ta đang xem xét. Thông số này quyết định độ dài và khả năng chứa đựng theo trục dọc của vật thể trong không gian ba chiều. Nếu chiều cao thay đổi, toàn bộ lượng không gian bên trong sẽ biến thiên theo một tỷ lệ thuận tương ứng với diện tích đáy.

Đơn vị đo lường chuẩn

Kết quả cuối cùng của phép toán luôn được thể hiện dưới dạng các đơn vị khối như mét khối hoặc centimet khối tùy vào quy mô. Sự đồng nhất về đơn vị giữa bán kính và chiều cao là điều kiện tiên quyết để đạt được con số thể tích khối trụ hoàn chỉnh.

Các bước xác định thể tích khối trụ qua ví dụ mẫu

Việc thực hiện các phép toán cần được tiến hành theo một trình tự logic để đảm bảo không bỏ sót bất kỳ biến số nào trong quá trình xử lý. Để đạt được kết quả chính xác, bạn nên thực hiện theo các bước hướng dẫn chi tiết dưới đây:

• Xác định trị số bán kính của mặt đáy bằng cách đo trực tiếp hoặc chia đôi đường kính hiện có của vật thể.
• Tiến hành đo đạc chiều cao nối liền hai mặt phẳng tròn bằng các dụng cụ đo chuẩn hóa như thước dây hoặc thước kẹp.
• Thực hiện phép tính bình phương bán kính để tìm ra giá trị diện tích đại diện cho phần đáy của hình trụ.
• Nhân kết quả vừa tìm được với hằng số pi để xác định diện tích bề mặt tròn một cách đầy đủ nhất.
• Lấy toàn bộ diện tích đáy vừa có nhân với chiều cao thực tế để cho ra con số thể tích khối trụ cuối cùng.
• Kiểm tra lại sự đồng nhất của các đơn vị đo lường để đảm bảo kết quả không bị sai lệch hàng chục hoặc hàng trăm lần.
• Ghi chú kết quả kèm theo đơn vị đo khối tương ứng để phục vụ cho các mục đích thống kê hoặc thi công tiếp theo.

Những lưu ý để tính thể tích khối trụ không sai sót

Trong quá trình thực hiện các phép toán, người thực hiện thường dễ mắc phải những lỗi cơ bản liên quan đến đơn vị hoặc thông số đầu vào. Dưới đây là bảng tổng hợp các thành phần tham gia vào quá trình tính toán để bạn có cái nhìn tổng quan nhất:

Thành phần	Ký hiệu đại diện	Đơn vị tính phổ biến	Vai trò trong phép tính
Bán kính đáy	r	m, cm, mm	Tạo ra diện tích bề mặt
Chiều cao	h	m, cm, mm	Tạo ra chiều sâu không gian
Số Pi	π\piπ	Không có	Hệ số chuyển đổi hình tròn
Thể tích	V	m3m3m3 , cm3cm3cm3 , lít	Kết quả dung tích cuối cùng

Đơn vị đo nhất quán

Sai lầm phổ biến nhất khi tính thể tích khối trụ chính là việc sử dụng các đơn vị đo khác nhau cho bán kính và chiều cao. Nếu bán kính được tính bằng centimet nhưng chiều cao lại dùng mét, kết quả sẽ hoàn toàn vô nghĩa và gây hậu quả nghiêm trọng. Bạn cần thực hiện việc quy đổi về cùng một hệ quy chiếu trước khi đặt các con số vào biểu thức toán học.

Phân biệt đường kính

Rất nhiều người nhầm lẫn giữa đường kính và bán kính khi đọc các bản vẽ kỹ thuật hoặc thông số sản phẩm công nghiệp. Công thức tính thể tích khối trụ mặc định sử dụng bán kính, vì vậy bạn phải luôn nhớ chia đường kính cho hai trước khi tính toán. Chỉ một sơ suất nhỏ này cũng có thể khiến kết quả của bạn lớn gấp bốn lần so với thực tế cần tìm.

Độ chính xác của pi

Tùy thuộc vào yêu cầu của công việc mà bạn nên chọn mức độ chi tiết của số pi sao cho phù hợp và hiệu quả nhất. Trong học thuật, việc giữ nguyên ký hiệu pi thường được khuyến khích để bảo toàn giá trị tuyệt đối cho bài toán thể tích khối trụ. Tuy nhiên, trong thực tế xây dựng, số 3,14 là đủ để mang lại độ tin cậy cho các công trình dân dụng thông thường.

Dưới đây là một số ví dụ thực tế giúp bạn hình dung rõ hơn về ứng dụng của công thức này:

1. Một bể nước hình trụ có bán kính đáy 1m và cao 2m sẽ chứa được khoảng 6,28 mét khối nước.
2. Một lon nước ngọt có bán kính 3cm và cao 12cm sẽ có thể tích khối trụ xấp xỉ 339 mililit.
3. Các cột trụ cầu đường với đường kính lớn đòi hỏi việc tính toán khối lượng bê tông cực kỳ khắt khe để đảm bảo an toàn.
4. Đường ống dẫn dầu xuyên quốc gia được tính toán dung tích dựa trên sự biến thiên của chiều dài ống.
5. Ngay cả những vật dụng nhỏ như bút chì hay viên phấn cũng mang cấu trúc hình học này.

Việc ứng dụng thể tích khối trụ vào sản xuất giúp doanh nghiệp tiết kiệm hàng tỷ đồng nhờ tối ưu hóa bao bì và vận chuyển. Khi bạn biết chính xác một vật thể chứa được bao nhiêu, bạn sẽ chủ động hơn trong việc sắp xếp kho bãi và logistics. Điều này chứng minh rằng toán học không hề khô khan mà trái lại rất thực tế và đầy quyền năng trong thế giới hiện đại khám phá thêm tại khí phách.

Kết luận

Thể tích khối trụ là một mảnh ghép kiến thức không thể thiếu giúp bạn chinh phục các bài toán hình học và ứng dụng thực tiễn một cách hiệu quả. Việc nắm vững công thức và các bước thực hiện sẽ mang lại sự tự tin cho bạn trong quá trình học tập cũng như làm việc chuyên môn. Hãy tiếp tục cập nhật thêm nhiều thông tin bổ ích và các mẹo tính toán nhanh tại trang tin của Khí Phách.